Уравнения прямой в пространстве. Уравнения прямой в пространстве - это уравнения двух пересекающихся плоскостей Уравнение прямой по которой пересекаются две плоскости

Канонические уравнения прямой

Постановка задачи. Найти канонические уравнения прямой, заданной как линия пересечения двух плоскостей (общими уравнениями)

План решения. Канонические уравнения прямой с направляющим вектором , проходящей через данную точку , имеют вид

. (1)

Поэтому, чтобы написать канонические уравнения прямой, необходимо найти ее направляющий вектор и какую-нибудь точку на прямой.

1. Так как прямая принадлежит одновременно обеим плоскостям, то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей, т.е. согласно определению векторного произведения, имеем

. (2)

2. Выбираем какую-нибудь точку на прямой. Поскольку направляющий вектор прямой не параллелен хотя бы одной из координатных плоскостей, то прямая пересекает эту координатную плоскость. Следовательно, в качестве точки на прямой может быть взята точка ее пересечения с этой координатной плоскостью.

3. Подставляем найденные координаты направляющего вектора и точки в канонические уравнения прямой (1).

Замечание. Если векторное произведение (2) равно нулю, то плоскости не пересекаются (параллельны) и записать канонические уравнения прямой не представляется возможным.

Задача 12. Написать канонические уравнения прямой.

Канонические уравнения прямой:

,

где – координаты какой-либо точки прямой, – ее направляющий вектор.

Найдем какую-либо точку прямой . Пусть , тогда

Следовательно, – координаты точки, принадлежащей прямой.

Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и, то есть как множество точек, удовлетворяющих системе двух линейных уравнений

(V.5)

Справедливо и обратное утверждение: система двух независимых линейных уравнений вида (V.5) определяет прямую как линию пересечения плоскостей (если они не параллельны). Уравнения системы (V.5) называются общим уравнением прямой в пространстве
.

Пример V .12 . Составить каноническое уравнение прямой, заданной общими уравнениями плоскостей

Решение . Чтобы написать каноническое уравнение прямой или, что тоже самое, уравнение прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например Oyz и Oxz .

Точка пересечения прямой с плоскостью Oyz имеет абсциссу
. Поэтому, полагая в данной системе уравнений
, получим систему с двумя переменными:

Ее решение
,
вместе с
определяет точку
искомой прямой. Полагая в данной системе уравнений
, получим систему

решение которой
,
вместе с
определяет точку
пересечения прямой с плоскостьюOxz .

Теперь запишем уравнения прямой, проходящей через точки
и
:
или
, где
будет направляющим векто-ром этой прямой.

Пример V .13. Прямая задана каноническим уравнением
. Составить общее уравнение этой прямой.

Решение. Каноническое уравнение прямой можно записать в виде системы двух независимых уравнений:



Получили общее уравнение прямой, которая теперь задана пересечением двух плоскостей, одна из которых
параллельна осиOz (
), а другая
– осиОу (
).

Данную прямую можно представить в виде линии пересечения двух других плоскостей, записав ее каноническое уравнение в виде другой пары независимых уравнений:



Замечание . Одна и та же прямая может быть задана различными системами двух линейных уравнений (то есть пересечением различных плоскостей, так как через одну прямую можно провести бесчисленное множество плоскостей), а также различными каноническими уравнениями (в зависимости от выбора точки на прямой и ее направляющего вектора).

Ненулевой вектор, параллельный прямой линии, будем называть ее направляющим вектором .

Пусть в трехмерном пространстве задана прямая l , проходящая через точку
, и ее направляющий вектор
.

Любой вектор
, где
, лежащий на прямой, коллинеарен с вектором, поэтому их координаты пропорциональны, то есть

. (V.6)

Это уравнение называется каноническим уравнением прямой. В частном случае, когда ﻉ есть плоскость, получаем уравнение прямой на плоскости

. (V.7)

Пример V .14. Найти уравнение прямой, проходящей через две точки
,
.

,

где
,
,
.

Удобно уравнение (V.6) записать в параметрической форме. Так как координаты направляющих векторов параллельных прямых пропорциональны, то, полагая

,

где t – параметр,
.

Расстояние от точки до прямой

Рассмотри двухмерное евклидовое пространство ﻉ с декартовой системой координат. Пусть точка
ﻉ и l ﻉ. Найдем расстояние от этой точки до прямой. Положим
, и прямая l задается уравнением
(рис.V.8).

Расстояние
, вектор
, где
– нормальный вектор прямой l ,
и – коллинеарны, поэтому их координаты пропорциональны, то есть
, следовательно,
,
.

Отсюда
или умножая эти уравнения наA и B соответственно и складывая их, находим
, отсюда

.

(V.8)

определяет расстояние от точки
до прямой
.

Пример V .15. Найти уравнение прямой, проходящей через точку
перпендикулярно прямойl :
и найти расстояние от
до прямойl .

Из рис. V.8 имеем
, а нормальный вектор прямойl
. Из условия перпендикулярности имеем

Так как
, то

. (V.9)

Это и есть уравнение прямой, проходящей через точку
,перпендикулярно прямой
.

Пусть имеем уравнение прямой (V.9), проходящей через точку
, перпендикулярна прямойl :
. Найдем расстояние от точки
до прямойl , используя формулу (V.8).

Для нахождения искомого расстояния достаточно найти уравнение прямой, проходящей через две точки
и точку
, лежащую на прямой в основании перпендикуляра. Пусть
, тогда

Так как
, а вектор
, то

. (V.11)

Поскольку точка
лежит на прямойl , то имеем еще одно равенство
или

Приведем систему к виду, удобному для применения метода Крамера

Ее решение имеет вид

,

. (V.12)

Подставляя (V.12) в (V.10), получаем исходное расстояние.

Пример V .16. В двухмерном пространстве задана точка
и прямая
. Найти расстояние от точки
до прямой; записать уравнение прямой, проходящей через точку
перпендикулярно заданной прямой и найти расстояние от точки
до основания перпендикуляра к исходной прямой.

По формуле (V.8) имеем

Уравнение прямой, содержащей перпендикуляр, найдем как прямую, проходящую через две точки
и
, воспользовавшись формулой (V.11). Так как
, то, с учетом того, что
, а
, имеем

.

Для нахождения координат
имеем систему с учетом того, что точка
лежит на исходной прямой

Следовательно,
,
, отсюда.

Рассмотрим трехмерное евклидовое пространство ﻉ. Пусть точка
ﻉ и плоскость ﻉ. Найдем расстояние от этой точки
до плоскости, заданной уравнением (рис.V.9).

Аналогично двухмерному пространству имеем
и вектор
, а, отсюда

. (V.13)

Уравнение прямой, содержащей перпендикуляр к плоскости , запишем как уравнение прямой, проходящей через две точки
и
, лежащую в плоскости:

. (V.14)

Для нахождения координат точки
к двум любым равенствам формулы (V.14) добавим уравнение

Решая систему трех уравнений (V.14), (V.15), найдем ,,– координаты точки
. Тогда уравнение перпендикуляра запишется в виде

.

Для нахождения расстояния от точки
до плоскости вместо формулой (V.13) воспользуемся

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

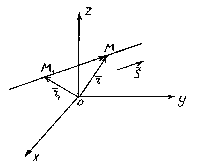
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

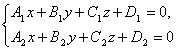
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

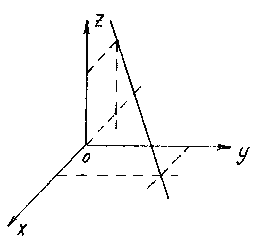
Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

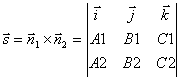Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Если две плоскости пересекаются, то система линейных уравнений задаёт уравнение прямой в пространстве .

То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:

Пример 9

Решение : Чтобы составить канонические уравнения прямой, необходимо знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….

1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? В системе уравнений нужно обнулить какую-нибудь координату. Пусть , тогда получаем систему двух линейных уравнений с двумя неизвестными: . Почленно складываем уравнения и находим решение системы:

Таким образом, точка принадлежит данной прямой. Обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует проводить мысленно или на черновике.

Выполним проверку: подставим координаты точки в исходную систему уравнений: . Получены верные равенства, значит, действительно .

2) Как найти направляющий вектор прямой? Его нахождение наглядно демонстрирует следующий схематический чертёж:

Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей. А если , то вектор «пэ» найдём как векторное произведение векторов нормали: .

Из уравнений плоскостей снимаем их векторы нормали:

И находим направляющий вектор прямой:

Как проверить результат, рассматривалось в статье Векторное произведение векторов .

3) Составим канонические уравнения прямой по точке и направляющему вектору :

Ответ :

На практике можно пользоваться готовой формулой: если прямая задана пересечением двух плоскостей , то вектор является направляющим вектором данной прямой.

Пример 10

Записать канонические уравнения прямой

Это пример для самостоятельного решения. Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения и подставьте в моё уравнение (или наоборот).

Полное решение и ответ в конце урока.

Во второй части урока мы рассмотрим взаимное расположению прямых в пространстве, а также разберём задачи, которые связаны с пространственными прямыми и точками. Терзают меня смутные ожидания, что материала будет прилично, поэтому лучше всё-таки сделать отдельную веб страницу.

Добро пожаловать: Задачи с прямой в пространстве >>>

Решения и ответы:

Пример 4: Ответы :

Пример 6: Решение : Найдём направляющий вектор прямой:

Уравнения прямой составим по точке и направляющему вектору :

Ответ : («игрек» – любое) :

Ответ :

Задача на пересечение плоскостей в силу своей важности носит у ряда авторов наименование «позиционная задача № 2».

Из стереометрии известно, что линией пересечения двух плоскостей служит прямая. В предыдущих предварительных задачах, где речь шла о частных случаях пересечения плоскостей, мы исходили из этого определения.

Как известно, чтобы построить ту или иную прямую, в простейшем случае требуется отыскать две точки, принадлежащие этой прямой. В случае задания плоскости следами в качестве этих двух точек выступают точки пересечения одноименных следов пересекающихся плоскостей.

Примеры для самостоятельной работы

Упражнение 5.1

Построить линии пересечения плоскостей, заданных следами (рис. 72):

• а) горизонтально проецирующей I и фронтально проецирующей А;
• б) горизонтально проецирующей Z и плоскости общего положения Q;
• в) двух плоскостей общего положения I и 0.

Рис. 72

На рис. 73 приведены ответы к этому упражнению.

Для случаев задания плоскостей локальными плоскими фигурами уместно использование по крайней мере двух различных путей решения.

Рис. 73

Первый путь решения - использование трехступенного алгоритма нахождения точки встречи прямой общего положения с плоскостью общего положения. Для нахождения линии пересечения двух треугольников один из треугольников оставляют без изменения, а второй мысленно расчленяют на отдельные отрезки, представляя их в качестве прямых общего положения. Сначала находят точку пересечения одной из прямых общего положения с плоскостью треугольника. Затем находят еще одну недостающую точку, принадлежащую искомой линии. Это делается аналогичным путем, повторяя всю описанную последовательность действий.

Упражнение 5.2

По заданным координатам вершин двух треугольников ЛВС и DEK построить эпюр последних и найти линию их пересечения. Указать видимость элементов обоих треугольников на эпюре: А (0, 9, 2); ?(10, 1, 16); С (23, 14, 9); D (3, 17, 18); ?(22, 11, 17); ?(12,0, 2). Для нахождения линий пересечения треугольников рекомендуется сначала найти точку встречи прямой KD с треугольником АВС, а затем точку встречи прямой СВ с треугольником EDK.

Общий вид полученного эпюра приведен на рис. 74.

Второй путь решения - использование двух вспомогательных секущих плоскостей уровня.

Заданные пересекающиеся плоские фигуры следует дважды пересечь вспомогательными плоскостями уровня (одноименными либо разноименными - безразлично), например двумя горизонтальными плоскостями уровня.

Нетрудно понять, что одноразовое рассечение позволяет отыскать две пересекающиеся прямые h l и И 2 , дающие одну точку А, принадлежащую искомой линии пересечения (рис. 75). Проводя еще одну аналогичную вспомогательную плоскость на некотором расстоянии

Рис. 74

Рис. 75

от первой, получают аналогичное построение и еще одну точку. Соединяя одноименные проекции двух полученных точек, находят искомую линию пересечения двух плоскостей.

Упражнение 5.3

По заданным координатам точек двух треугольных фигур построить эпюр последних, на котором построить с использованием вспомогательных плоскостей линию пересечения треугольников. Указать видимость элементов обоих треугольников на эпюре:

к АВС. А (16, 5, 17); Я (10, 19,

A DEF: D (24, 12, 14); ? (4, 18,

Общий вид решенной задачи изображен на рис. 76.

Упражнение 5.4

Для закрепления навыков нахождения линии пересечения двух плоскостей приводится задача, решение которой дается в динамике построений в соответствии со ступенями алгоритма.

Найти линию пересечения двух плоскостей общего положе- р ис jq

ния, заданных двумя треугольниками АВС и DEF, и определить видимость их взаимопроникновения (рис. 77).

Решение примера сводится к отысканию точек пересечения сторонами (прямыми) ААВС с плоскостью общего положения, заданной ADEF. Алгоритм решения этого примера известен.

Заключаем сторону (прямую) АС ЬЛВС во вспомогательную фронтально проецирующую плоскость т _1_ П 2 (рис. 78).

Фронтальный след этой вспомогательной плоскости пересекает проекции сторон D 2 E 2 глЕ 2 - 1 2 и D 2 F 2 пт 2 = 2 2 в точках 1 2 и 2 2 . Проекционные линии связи позволяют на горизонтальной плоскости проекций определить линию пересечения (1 !~2 2) = n AD X E X F { . Тогда точка К 1 и ее проекция К 2 определяют точку пересечения прямой АС с ADEF.

Повторяем алгоритм нахождения точки пересечения стороны ААВС прямой ВС с ADEF. Заключаем ВС во вспомогательную фронтально проецирующую плоскость р _L П 2 (рис. 79).

Находим проекции точек 3 и 4 и на горизонтальной плоскости проекций определяем проекцию точки пересечения прямой В 1 С [ с линией пересечения (3,-4,):

Проекционная линия связи позволяет найти ее фронтальную проекцию точку М 2 .

Соединяем найденные точки Ки Ми находим линию пересечения двух плоскостей общего положения AABC n ADEF= АЖ (рис. 80).

Видимость сторон ААВС относительно ADEF определяется с помощью конкурирующих точек. Сначала определяем видимость геометрических фигур на плоскости проекций П 2 . Для этого через конкурирующие точки 5 и 6 (5 2 = 6 2) проводим проекционную линию связи, перпендикулярную оси проекций х п (рис. 81).

По горизонтальным проекциям 5 У и 6 { точек 5 и 6, в которых линия проекционной связи соответственно пересекает скрещивающиеся прямые АС 4 DF, выясняется, что точка 6 более удалена от плоскости проекций П 2 , чем точка 5. Поэтому точка 6 и прямая DF, которой она принадлежит, видимы относительно плоскости проекций П 2 . Отсюда следует, что отрезок (К 2 -6 2) будет невидимым. Аналогично определяем видимость сторон АЛВС и ADEF - ВС и DF, т.е. отрезок (Ж 2 -8 2) будет невидимым.

Видимость ААВС и ADEF относительно плоскости проекций П j, устанавливается аналогично. Для определения видимости скрещивающихся прямых АС * DF и ВС ±DF относительно плоскости проекций П] через конкурирующие точки 9 1 = 10 1 и11 1 = 12 1 проводим проекционные линии связи перпендикулярно х п. По фронтальным проекциям этих конкурирующих точек устанавливаем, что проекции точек 10 2 и 12 2 более удалены от плоскости проекций П { . Следовательно, отрезки (А^-ЮД и (М г 2 1) будут невидимыми. Отсюда видимость ААВС и ADEF наглядно представлена на рис. 82.