Габриель Крамер – математик, создатель одноименного метода решения систем линейных уравнений
Габриель Крамер – известный математик, который родился 31 июля 1704 года. Ещё в детстве Габриель поражал своими интеллектуальными способностями, особенно в области математики. Когда Крамеру было 20 лет, он устроился в Женевский университет штатным преподавателем.
Во время путешествия по Европе Габриель познакомился с математиком Иоганном Бернулли, который и стал его наставником. Только благодаря Иоганну, Крамер написал много статей по геометрии, истории математики и философии. А в свободное от работы время изучал математику всё больше и больше.
Наконец-то наступил тот день, когда Крамер нашёл способ, при помощи которого можно было бы легко решать не только лёгкие, но и сложные системы линейных уравнений.
В 1740 году у Крамера были опубликованы несколько работ, где доступно изложено решение квадратных матриц и описан алгоритм, как находить обратную матрицу . Далее математик описывал нахождения линейных уравнений разной сложности, где можно применить его формулы. Поэтому тему так и назвали: «Решение систем линейных уравнений методом Крамера».
Учёный умер в возрасте 48 лет (в 1752 году). У него было ещё много планов, но, к сожалению, он так и не успел их осуществить.
Пусть дана система линейных уравнений такого вида:
где , , – неизвестные переменные, – это числовые коэффициенты, в – свободные члены.
Решением СЛАУ (систем линейных алгебраических уравнение) называются такие неизвестные значения при которых все уравнения данной системы преобразовываются в тождества.
Если записать систему в матричном виде, тогда получается , где
В данной главной матрице находятся элементы, коэффициенты которых при неизвестных переменных,
Это матрица-столбец свободных членов, но есть ещё матрица-столбец неизвестных переменных:
После того, когда найдутся неизвестные переменные, матрица и будет решением системы уравнений, а наше равенство преобразовывается в тождество. . Если умножить , тогда . Получается: .
Если матрица – невырожденная, то есть, её определитель не равняется нулю, тогда у СЛАУ есть только одно единственное решение, которое находится при помощи метода Крамера.
Как правило, для решения систем линейных уравнений методом Крамера, нужно обращать внимания на два свойства, на которых и основан данный метод:
1. Определитель квадратной матрицы равняется сумме произведений элементов любой из строк (столбца) на их алгебраические дополнения:
Здесь – 1, 2, …, n; – 1, 2, 3, …, n.
2. Сумма произведений элементов данной матрицы любой строки или любого столбца на алгебраические дополнения определённых элементов второй строки (столбца) равняется нулю:
где – 1, 2, …, n; – 1, 2, 3, …, n. .
Итак, теперь можно найти первое неизвестное . Для этого необходимо умножить обе части первого уравнения системы на , части со второго уравнения на , обе части третьего уравнения на и т. д. То есть, каждое уравнение одной системы нужно умножать на определённые алгебраические дополнения первого столбца матрицы :
Теперь прибавим все левые части уравнения, сгруппируем слагаемые, учитывая неизвестные переменные и приравняем эту же сумму к сумме правых частей системы уравнения:
Можно обратиться к вышеописанным свойствам определителей и тогда получим:
И предыдущее равенство уже выглядит так:
Откуда и получается .
Аналогично находим . Для этого надо умножить обе части уравнений на алгебраические дополнения, которые находятся во втором столбце матрицы .
Теперь нужно сложить все уравнения системы и сгруппировать слагаемые при неизвестных переменных. Для этого вспомним свойства определителя:
Откуда получается .
Аналогично находятся все остальные неизвестные переменные.
Если обозначить:
тогда получаются формулы, благодаря которым находятся неизвестные переменные методом Крамера:
Замечание.
Тривиальное решение при может быть только в том случае, если система уравнений является однородной . И действительно, если все свободные члены нулевые, тогда и определители равняются нулю, так как в них содержится столбец с нулевыми элементами. Конечно же, тогда формулы , , дадут
Метод Крамера – теоремы
Прежде чем решать уравнение, необходимо знать:
- теорему аннулирования;
- теорему замещения.
Теорема замещения
Теорема
Сумма произведений алгебраических дополнений любого столбца (строки) на произвольные числа равняется новому определителю, в котором этими числами заменены соответствующие элементы изначального определителя, что отвечают данным алгебраическим дополнениям.
Например,
где – алгебраические дополнения элементов первого столбца изначального определителя:
Теорема аннулирования
Теорема
Сумма произведений элементов одной строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равняется нулю.
Например:
Алгоритм решения уравнений методом Крамера
Метод Крамера – простой способ решения систем линейных алгебраических уравнений. Такой вариант применяется исключительно к СЛАУ, у которых совпадает количество уравнений с количеством неизвестных, а определитель отличен от нуля.
Итак, когда выучили все этапы, можно переходить к самому алгоритму решения уравнений методом Крамера. Запишем его последовательно:
Шаг 1. Вычисляем главный определитель матрицы
и необходимо убедиться, что определитель отличен от нуля (не равен нулю).
Шаг 2. Находим определители
Это и есть определители матриц, которые получались из матрицы при замене столбцов на свободные члены.
Шаг 3. Вычисляем неизвестные переменные
Теперь вспоминаем формулы Крамера, по которым вычисляем корни (неизвестные переменные):
Шаг 4. Выполняем проверку
Выполняем проверку решения при помощи подстановки в исходную СЛАУ. Абсолютно все уравнения в системе должны быть превращены в тождества. Также можно высчитать произведение матриц . Если в итоге получилась матрица, которая равняется , тогда система решена правильно. Если же не равняется , скорей всего в одном из уравнений есть ошибка.
Давайте для начала рассмотрим систему двух линейных уравнений, так как она более простая и поможет понять, как правильно использовать правило Крамера. Если вы поймёте простые и короткие уравнения, тогда сможете решить более сложные системы трёх уравнений с тремя неизвестными.
Кроме всего прочего, есть системы уравнений с двумя переменными, которые решаются исключительно благодаря правилу Крамеру.
Итак, дана система двух линейных уравнений:
Для начала вычисляем главный определитель (определитель системы):
Значит, если , тогда у системы или много решений, или система не имеет решений. В этом случае пользоваться правилом Крамера нет смысла, так как решения не получится и нужно вспоминать метод Гаусса , при помощи которого данный пример решается быстро и легко.
В случае, если , тогда у система есть всего одно решение, но для этого необходимо вычислить ещё два определителя и найти корни системы.
Часто на практике определители могут обозначаться не только , но и латинской буквой , что тоже будет правильно.
Корни уравнения найти просто, так как главное, знать формулы:
Так как мы смогли решить систему двух линейных уравнений, теперь без проблем решим и систему трёх линейных уравнений, а для этого рассмотрим систему:
Здесь алгебраические дополнения элементов – первый столбец . Во время решения не забывайте о дополнительных элементах. Итак, в системе линейных уравнений нужно найти три неизвестных – при известных других элементах.
Создадим определитель системы из коэффициентов при неизвестных:
Умножим почленно каждое уравнение соответственно на , , – алгебраические дополнения элементов первого столбца (коэффициентов при ) и прибавим все три уравнения. Получаем:
Согласно теореме про раскладывание, коэффициент при равняется . Коэффициенты при и будут равняться нулю по теореме аннулирования. Правая часть равенства по теореме замещения даёт новый определитель, который называется вспомогательным и обозначается
После этого можно записать равенство:
Для нахождения и перемножим каждое из уравнений изначальной системы в первом случае соответственно на , во втором – на и прибавим. Впоследствии преобразований получаем:
Если , тогда в результате получаем формулы Крамера:
Порядок решения однородной системы уравнений
Отдельный случай – это однородные системы:
Среди решений однородной системы могут быть, как нулевые решения , так и решения отличны от нуля.
Теорема
Если определитель однородной системы (3) отличен от нуля , тогда у такой системы может быть только одно решение.
Действительно, вспомогательные определители , как такие у которых есть нулевой столбец и поэтому, за формулами Крамера
Теорема
Если у однородной системы есть отличное от нуля решение, тогда её определитель равняется нулю
Действительно, пусть одно из неизвестных, например, , отличное от нуля. Согласно с однородностью Равенство (2) запишется: . Откуда выплывает, что
Примеры решения методом Крамера
Рассмотрим на примере решение методом Крамера и вы увидите, что сложного ничего нет, но будьте предельно внимательно, так как частые ошибки в знаках приводят к неверному ответу.
Пример 1
Задача
Решение
Первое, что надо сделать – вычислить определитель матрицы:
Как видим, , поэтому по теореме Крамера система имеет единственное решение (система совместна). Далее нужно вычислять вспомогательные определители. Для этого заменяем первый столбец из определителя на столбец свободных коэффициентов. Получается:
Аналогично находим остальные определители:
И проверяем:
Ответ
Пример 2
Задача
Решить систему уравнений методом Крамера:
Решение
Находим определители:
Ответ
= = = = = =
Проверка
Уравнение имеет единственное решение.
Ответ
Пример 3
Задача
Решить систему методом Крамера
Решение
Как вы понимаете, сначала находим главный определитель:
Как мы видим, главный определитель не равняется нулю и поэтому система имеет единственное решение. Теперь можно вычислить остальные определители:
При помощи формул Крамера находим корни уравнения:
Чтобы убедиться в правильности решения, необходимо сделать проверку:
Как видим, подставив в уравнение решённые корни, у нас ответ получился тот же, что и в начале задачи, что говорит о правильном решении уравнений.
Ответ
Система уравнений имеет единственное решение: , , .
Есть примеры, когда уравнение решений не имеет. Это может быть в том случае, когда определитель системы равен нулю, а определители при неизвестных неравны нулю. В таком случае говорят, что система несовместна, то есть не имеет решений. Посмотрим на следующем примере, как такое может быть.
Пример 4
Задача
Решить систему линейных уравнений методом Крамера:
Решение
Как и в предыдущих примерах находим главный определитель системы:
В этой системе определитель равняется нулю, соответственно, система несовместна и определенна или же несовместна и не имеет решений. Чтобы уточнить, надо найти определители при неизвестных так, как мы делали ранее:
Мы нашли определители при неизвестных и увидели, что все они не равны нулю. Поэтому система несовместна и не имеет решений.
Ответ
Система не имеет решений.
Часто в задачах на системы линейных уравнений встречаются такие уравнения, где есть не одинаковые буквы, то есть, кроме букв, которые обозначают переменные, есть ещё и другие буквы и они обозначают некоторое действительное число. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. Давайте и рассмотрим такой пример.
Используя формулы Крамера, находим:
Ответ
И наконец, мы перешли к самой сложной системе уравнений с четырьмя неизвестными. Принцип решения такой же, как и в предыдущих примерах, но в связи с большой системой можно запутаться. Поэтому рассмотрим такое уравнение на примере.
В изначальном определители из элементов второй строки мы отнимали элементы четвёртой строки, а из элементов третьей строки отнимались элементы четвёртой строки, которые умножались на 2. Также отнимали из элементов четвёртой строки элементы первой строки, умноженной на два. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Теперь можно находить определители при неизвестных:
Для преобразований определителя при четвёртом неизвестном из элементов первой строки мы вычитали элементы четвёртой строки.
Теперь по формулам Крамера нужно найти:
Ответ
Итак, мы нашли корни системы линейного уравнения:
Подведём итоги
При помощи метода Крамера можно решать системы линейных алгебраических уравнений в том случае, если определитель не равен нулю. Такой метод позволяет находить определители матриц такого порядка, как на благодаря формулам Крамера, когда нужно найти неизвестные переменные. Если все свободные члены нулевые, тогда их определители равны нулю, так как в них содержится столбец с нулевыми элементами. И конечно же, если определители равняются нулю, лучше решать систему методом Гаусса Метод Крамера в Excel от 2007 (XLSX)
Метод Крамера – теорема, примеры решений обновлено: 22 ноября, 2019 автором: Научные Статьи.Ру
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
 ;
;
 .
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:


Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ![]() ,
,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
 .
.
На основании теоремы Крамера
………….
,
где -
-
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:



Пример 2.
 .
.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители


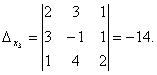
По формулам Крамера находим:
![]()
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
 .
.
Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных



По формулам Крамера находим:
Итак, решение системы - (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных



Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных - буквы. За примерами далеко ходить не надо.
Следующий пример - на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

В § 3.3 были показаны ограничения, возникающие при слежении за сигналами изменяющейся частоты при помощи системы второго порядка. Рассмотрим теперь возможность смягчения некоторых из этих ограничений путем введения в систему второго интегратора. Оказывается, что процесс захвата для системы третьего порядка менее устойчив, чем для системы второго порядка, но при помощи второго интегратора можио расширить диапазон слежения за системой, которая в начальный момент была уже захвачена. Передаточная функция фильтра теперь имеет вид
и из (3.1) следует:

После подстановки это выражение приводится к виду

Нормируя и вводя обозначения получим
Обычный метод фазовой плоскости неприменим к дифференциальным уравнениям третьего порядка вследствие того, что в этом случае имеются три начальных условия, соответствующие трем переменным: фазе, частоте и скорости изменения частоты (в механических системах - смещению, скорости и ускорению). В принципе траектории, определяемые уравнением третьего порядка, можно было бы представить в трехмерном пространстве. Всякая же попытка спроектировать эти траектории для J множества начальных условий на плоскость привела бы к столь запутанной диаграмме, что из нее было бы невозможно сделать какие-либо общие заключения.
С другой стороны, если ограничиться одной совокупностью начальных условий, то можно получить проекцию траектории на плоскость . Особое значение представляет следующая совокупность начальных условий: Другими словами, система в начальный момент захвачена, так что ошибки по частоте и фазе равны нулю, когда опорная частота начинает линейно изменяться.
Легко изменить структуру аналоговоговычислительного устройства, чтобы учесть введение второго интегратора.
Рис. 3.19. Проекции траекторий в фазовом пространстве для петли третьего порядка
(см. скан)
На рис. 3.19 изображен ряд траекторий, спроектированных на плоскость . Во всех рассмотренных случаях так что . В гипотетическом трехмерном «фазовом пространстве» траектории начинаются в точке и заканчиваются на оси
На рис. 3.19, а показано поведение системы второго порядка при таких же начальных условиях. Окончательное, или установившееся, значение фазы равно как было показано в § 3.3. Введение второго интегратора приводит к уменьшению установившейся ошибки по фазе до нуля тем быстрее, чем больше При возрастании наибольшая ошибка по фазе также уменьшается, однако за счет уменьшения затухания системы, что приводит к увеличению среднеквадратичной ошибки по фазе (см. рис. 3.19, б - 3.19, ж). Наконец, при система становится неустойчивой.
Получаемое путем увеличения порядка системы улучшение иллюстрируется на рис. 3.20. Здесь как и прежде, но . В § 3.3 было показано, что при такой или большей быстроте линейного изменения частоты система не могла осуществлять слежение. Рис. 3.20, а подтверждает это обстоятельство. С другой стороны, даже при наименьшей степени влияния второго интегратора получается нулевая установившаяся ошибка по фазе. Наибольшее мгновенное значение фазового рассогласования уменьшается при увеличении коэффициента но при система вновь делается неустойчивой.
Аналогичные особенности видны на рис. 3.21-3.23, за исключением того обстоятельства, что при возрастании отношения для поддержания системы в состоянии захвата требуются все возрастающие значения коэффициента В конце концов при приближении отношения к 2 или при необходимо, чтобы было около 1/2. Но из рис. 3.19, ж - 3.23, з видно, что при этом значении система неустойчива. Диапазон значений коэффициента при которых система остается в состоянии захвата в зависимости от отношения представлен на рис. 3.24-3.26 при значениях соответственно. Заштрихована область допустимых значений коэффициента Видно, что при линейном изменении частоты введение системы третьего порядка позволило расширить Диапазон, при котором получается слежение, примерно
Рис. 3.20. Проекции траекторий в фазовом пространстве для петли третьего порядка
(см. скан)
Рис. 3.21. Проекции траекторий в фазовом пространстве для петли третьего порядка
(см. скан)
Рис. 3.22. Проекции траекторий в фазовом пространстве для петли третьего порядка
(см. скан)
Рис. 3.23. Проекции траекторий в фазовом пространстве для петли третьего порядка
(см. скан)

Рис. 3.24. Область состояния захвата системы третьегопорядка

Рис. 3.25. Область состояния захвата системы третьего порядка

Рис. 3.26. Область состояния захвата системы третьего порядка
вдвое больше по сравнению с системой второго порядка при и даже еще большее при меньших значениях
Можно теоретически объяснить колебательный характер изменения коэффициента b при его значениях около или более 1/2. Продифференцировав уравнение (3.41), получим
Для более глубокого понимания происходящего в этой статье можно ознакомиться с .Рассмотрим однородную систему дифференциальных уравнений третьего порядка
Здесь x(t), y(t), z(t) - искомые функции на промежутке (a, b), a ij (i, j =1, 2, 3) - вещественные числа.
Запишем исходную систему в матричном виде
,
где
Решение исходной системы будем искать в виде
,
где ![]() , C 1 , C 2 , C 3 - произвольные постоянные.
, C 1 , C 2 , C 3 - произвольные постоянные.
Чтобы найти фундаментальную систему решений, нужно решить так называемое характеристическое уравнение
Это уравнение является алгебраическим уравнением третьего порядка, следовательно оно имеет 3 корня. При этом возможны следующие случаи:
1. Корни (собственные значения) действительны и различны.
2. Среди корней (собственных значений) есть комплексно-сопряженные, пусть
- действительный корень
=
3. Корни (собственные значения) действительны. Один из корней кратный.
Чтобы разобраться, как действовать в каждом из этих случаев, нам понадобятся:
Теорема 1.
Пусть - попарно различные собственные значения матрица А, а - соответствующие им собственные векторы. Тогда
образуют фундаментальную систему решений исходной системы.
Замечание
.
Пусть - действительное собственное значение матрица А (действительный корень характеристического уравнения), - соответствующий ему собственный вектор.
= - комплексные собственные значения матрицы А, - соответствующий - собственный вектор. Тогда
(Re - действительная часть, Im - мнимая)
образуют фундаментальную систему решений исходной системы. (Т.е. и = рассматриваются вместе)
Теорема 3.
Пусть - корень характеристического уравнения кратности 2. Тогда исходная система имеет 2 линейно независимых решения вида![]() ,
,
где , - постоянные вектора. Если же кратности 3, то существует 3 линейно независимых решения вида
.
Векторы находятся подствалением решений (*) и (**) в исходную систему.
Чтобы лучше понять метод нахождения решений вида (*) и (**), смотри разобранные типичные примеры ниже.
Теперь рассмотрим более подробно каждый из вышеописанных случаев.
1. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае различных действительных корней характеристического уравнения.
Дана система
1) Составляем характеристическое уравнение
- действительные и различные собственные значения 9корни этого уравнения).
2)Строим , где
3)Строим , где
- собственный вектор матрицы А, соответствующий , т.е. - любое решение системы
4)Строим , где
- собственный вектор матрицы А, соответствующий , т.е. - любое решение системы
5)
составляют фундаментальную систему решений. Далее записываем общее решение исходной системы в виде
,
здесь C 1 , C 2 , C 3 - произвольные постоянные,
,
или в координатном виде
Расмотрим несколько примеров:
Пример 1.
![]()

2) Находим
3)Находим
4)Вектор-функции![]()
![]()
или в координатной записи
Пример 2.

1)Составляем и решаем характеристическое уравнение:
2) Находим
3)Находим
4)Находим
5)Вектор-функции
образуют фундаментальную систему. Общее решение имеет вид
или в координатной записи
2. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае комплексно-сопряженных корней характеристического уравнения.
- действительный корень,
2)Строим , где
3) Строим
| - собственный вектор матрицы А, соответствующий , т.е. удовлетворяет системе |
Здесь Re - действительная часть
Im - мнимая часть
4) составляют фундаментальную систему решений. Далее записываем общее решение исходной системы:
, где
С 1 , С 2 ,С 3 произвольные постоянные.
Пример 1.

1) Составляем и решаем характеристическое уравнение
2)Строим

3) Строим
, где

Первое уравнение сократим на 2. Затем ко второму уравнению прибавим первое, умноженное на 2i, а от третьего уравнения отнимем перове, умноженное на 2.
Далее
Следовательно,
4) - фундаментальная система решений. Запишем общее решение исходной системы:
Пример 2.
![]()
1) Составляем и решаем харктеристическое уравнение
2)Строим
(т.е. и рассматриваем вместе), где

Второе уравнение умножим на (1-i) и сократим на 2.

Следовательно,![]()
3)
Общее решение исходной системы
или
2. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае кратных корней характеристического уравнения.
Составляем и решаем характеристическое уравнение
Возможны два случая:![]()
Рассмотрим случай а) 1) , где
| - собственный вектор матрицы А, соответствующий , т.е удовлетворяет системе |
2) Сошлемся на Теорему 3, из которой следует, что существуют два линейно независимых решения вида![]() ,
,
где , - постоянные векторы. Их возьмем за .
3) - фундаментальная система решений. Далее записываем общее решение исходной системы:
Рассмотрим случай б):
1) Сошлемся на Теорему 3, из которой следует, что существует три линейно независимых решения вида
,
где , , - постоянные векторы. Их возьмем за .
2) - фундаментальная система решений. Далее записываем общее решение исходной системы.
Чтобы лучше понять как находить решения вида (*), рассмотрим несколько типичных примеров.
Пример 1.

Составляем и решаем характеристическое уравнение:
Имеем случай а)
1) Строим , где
, где

Из второго уравнения вычитаем первое:
 ? третья строка подобна второй, ее вычеркиваем. Из первого уравнения вычтем второе:
? третья строка подобна второй, ее вычеркиваем. Из первого уравнения вычтем второе:
2) = 1 (кратность 2)
Этому корню по Т.3 должно соответствовать два линейно независимых решения вида .
Попробуем найти все линейно незваисимые решения, у которых , т.е. решения вида
.
Такой вектор будет решением тогда и только тогда, когда - собственный вектор, соответствующий =1, т.е.
, или , вторая и третья строки подобны первой, выкидываем их.
, вторая и третья строки подобны первой, выкидываем их.![]()
Система свелась к одному уравнению. Следовательно, имеется два свободных неизвестных, например, и . Дадим им сначала значения 1, 0; потом значения 0, 1. Получим такие решения: .
.
Следовательно,  .
.
3) - фундаментальная система решений. Осталось записать общее решение исходной системы: .
.. Таким образом существует только одно решение вида
Подставим X 3 в эту систему:
Вычеркнем третью строку (она подобна второй). Система совместна (имеет решение) при любом с. Пусть с=1.
.
.. Таким образом существует только одно решение вида
Подставим X 3 в эту систему:
Вычеркнем третью строку (она подобна второй). Система совместна (имеет решение) при любом с. Пусть с=1.
или
Курсовая: Определители и системы линейных уравнений
1. Определители второго и третьего порядков и их свойства
1.1. Понятие матрицы и определителя второго порядка
Прямоугольную таблицу из чисел,
матрицей. Для обозначения матрицы используют либо сдвоенные вертикальные
черточки, либо круглые скобки. Например:
1 7 9.2 1 7 9.2
28 20 18 28 20 18
6 11 2 -6 11 2
Если число строк матрицы совпадает с числом ее столбцов, то матрица называется
квадратной. Числа, входящие в состав матрицы, называют ее элементами .
Рассмотрим квадратную матрицу, состоящую из четырех элементов:
Определителем второго порядка, соответствующим матрице (3.1), называется число,
и обозначаемое символом
Итак, по определению
Элементы, составляющие матрицу данного определителя, обычно называют
элементами этого определителя.
Справедливо следующее утверждение: для того чтобы определитель второго
порядка был равен нулю, необходимо и достаточно, чтобы элементы его строк (или
соответственно его столбцов) были пропорциональны .
Для доказательства этого утверждения достаточно заметить, что каждая из
пропорций /
эквивалентна равенству
А последнее равенство в силу (3.2) эквивалентно обращению в нуль определителя.
1.2. Система двух линейных уравнений с двумя неизвестными
Покажем, как применяются определители второго порядка для исследования и
отыскания решений системы двух линейных уравнений с двумя неизвестными
(коэффициенты ,
и свободные члены ,
считаются при этом заданными). Напомним, что пара чисел
Называется
решением системы (3.3), если подстановка этих чисел на место
и в данную систему
обращает оба уравнения (3.3) в тождества.
Умножая первое уравнение системы (3.3) на -
А второе - на -и
затем складывая полученные при этом равенства, получим
Аналогично путем умножения уравнений (3.3) на -исоответственно получим:
Введем следующие обозначения:
С помощью этих обозначений и выражения для определителя второго порядка
уравнения (3.4) и (3.5) могут быть переписаны в виде:
Определитель ,
составленный из коэффициентов при неизвестных системы (3.3), принято называть
определителем этой системы . Заметим, что определители
и получаются из
определителя системы
посредством замены его первого или соответственно второго столбца свободными
Могут представиться два случая: 1) определитель системы
отличен от нуля; 2) этот определитель равен нулю.
Рассмотрим сначала случай
0. Из уравнений (3.7) мы сразу же получаем формулы для неизвестных,
называемые формулами Крамера :
Полученные формулы Крамера (3.8) дают решение системы (3.7) и потому доказывают
единственность решения исходной системы (3.3). В самом деле, система (3.7)
является следствием системы (3.3), поэтому всякое решение системы (3.3) (в
случае, если оно существует!) должно являться решением и системы (3.7). Итак,
пока доказано, что если у исходной системы (3.3) существует при
0 решение, то это решение однозначно определяется формулами Крамера (3.8).
Легко убедиться и в существовании решения, т. е. в том. что при
0 два числа и
Определяемые формулами Крамера (3.8). будучи поставлены на место неизвестных в
уравнения (3.3), обращают эти уравнения в тождества. (Предоставляем читателю
самому расписать выражения для определителей
И убедиться в справедливости указанных тождеств.)
Мы приходим к следующему выводу: если определитель
системы (3.3) отличен от нуля, то существует, и притом единственное решение этой
системы, определяемое формулами Крамера (3.8).
Рассмотрим теперь случай, когда определитель
системы равен нулю . Могут представиться два подслучая : а) хотя
бы один из определителей
или , отличен от
нуля; б) оба определителя
и равны нулю. (если
определитель и
один из двух определителей
и равны нулю, то и
другой из указанных двух определителей равен нулю. В самом деле, пусть,
например = 0
Тогда из этих пропорций получим, что
В подслучае а) оказывается невозможным хотя бы одно из равенств (3.7), т. е.
система (3.7) не имеет решений, а поэтому не имеет решений и исходная система
(3.3) (следствием которой является система (3.7)).
В подслучае б) исходная система (3.3) имеет бесчисленное множество решений. В
самом деле, из равенств
0 и из утверждения в конце разд. 1.1 заключаем, что второе уравнение системы
(3.3) является следствием первого и его можно отбросить. Но одно уравнение с
двумя неизвестными
имеет бесконечно много решений (хотя бы один из коэффициентов
Или отличен от
нуля, и стоящее при нем неизвестное может быть определено из уравнения (3.9)
через произвольно заданное значение другого неизвестного).
Таким образом, если определитель
системы (3.3) равен нулю, то система (3.3) либо вовсе не имеет решений (в
случае, если хотя бы один из определителей
или отличен от
нуля), либо имеет бесчисленное множество решений (в случае, когда
0). В последнем
случае два уравнения (3.3) можно заменить одним и при решении его одно
неизвестное задавать произвольно.
Замечание . В случае, когда свободные члены
и равны нулю,
линейная система (3.3) называется однородной . Отметим, что однородная
система всегда имеет так называемое тривиальное решение:
0, = 0 (эти два
числа обращают оба однородных уравнения в тождества).
Если определитель однородной системы
отличен от нуля, то эта система имеет только тривиальное решение. Если же
= 0, то однородная система имеет бесчисленное множество решений (поскольку
для однородной системы возможность отсутствия решений исключена). Таким
образом, однородная система имеет нетривиальное решение в том и только в
том случае, когда определитель ее равен нулю.



